数独技巧教程01 - 数独介绍

数独介绍

数独游戏的起源可以追溯到18世纪，最初的版本是在瑞士数学家约翰·霍普克罗夫特（Leonhard Euler）提出的“拉丁方阵”基础上发展而来的。尽管数独的现代形式是在20世纪后期才流行开来，但它的根源可以追溯到这些早期的数学研究。

现代数独的雏形出现在1979年，由美国的报纸设计师霍华德·加恩斯（Howard Garns）创建。他为《米尔沃基日报》设计了一种名为“数字方阵”的游戏，后来被称为数独。1984年，日本的出版公司把这种游戏引入日本，并赋予了“数独”这个名字，意为“单一的数字”。此后，数独在日本迅速流行，成为了一种广受欢迎的智力游戏。

进入21世纪后，数独在全球范围内爆炸性增长，成为报纸、杂志和各种在线平台上常见的益智游戏。数独不仅考验玩家的逻辑推理能力，还培养了耐心和专注力，使其成为了一种深受各年龄层欢迎的休闲活动。如今，数独的变种和挑战层出不穷，吸引了无数爱好者投身其中。

基本规则

数独盘面是一个像上面这样 9*9 的正方形，每行、每列各 9 个小格，总共 81 格

每 9 个小格组成的一个大方块称为宫，盘面总共有 9 宫

数独的基本规则就是要在每行、每列、每宫中都填上 1 到 9 的数字，且每行、每列、每宫的数字不能重复

下面这个是一个已经填好的数独盘面，可以观察下每行、每列、每宫，都是 1 到 9 的数字，且没有重复

每道标准的数独题目都只有唯一解，而且解题过程不需要进行猜测，都可以通过推理得出正确的结果

等位群格位

每个格子填上数字后同一行、列、宫的其他格子都不能有这个数字，总共有 20 格，称为等位群格位（或称为影响区域）

每个空格子都可以通过检查它的等位群格位（影响区域）已有的数字来进行排除，如果只剩 1 个可填的数字就可以直接填入

强弱关系

除了常见的排除法外，强弱关系是数独中最基础的推理理论，很多高级技巧都基于强弱关系

我们先将所有格的候选数都填上，现在来看数字1

在第 2 宫中，数字 1 只可能在两个位置：R2C5 和 R3C6，如果不在 R2C5 就一定在 R3C6，反之亦然。这种“非此即彼”的关系称为强关系

R3C6 和 R3C8 同样也是这种关系

在第 2 行中，数字 1 可以在三个位置：R2C5、R2C8 和 R2C9，如果 1 在 R2C5，那么 R2C8 和 R2C9 就一定不是数字 1，这种“在此非彼”的关系称为弱关系

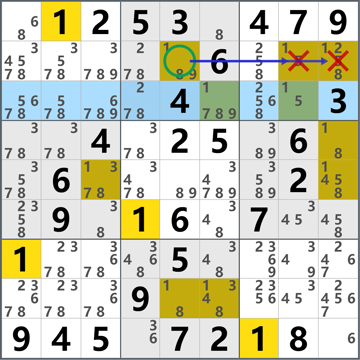
R2C9 和 R2C8、R3C8 同样也是这种关系

另外，“非此即彼”的强关系也具有“在此非彼”弱关系性质，所以在实际推理中，强关系也可以当做弱关系使用

强弱关系交替组合可以组成强弱链进行推理，可以查看后续的单数链和双数链方法了解详情